基础矩阵求解

最近在重新温故双目视觉相关的知识，此篇讲解对极几何、基础矩阵等相关知识。

对极几何

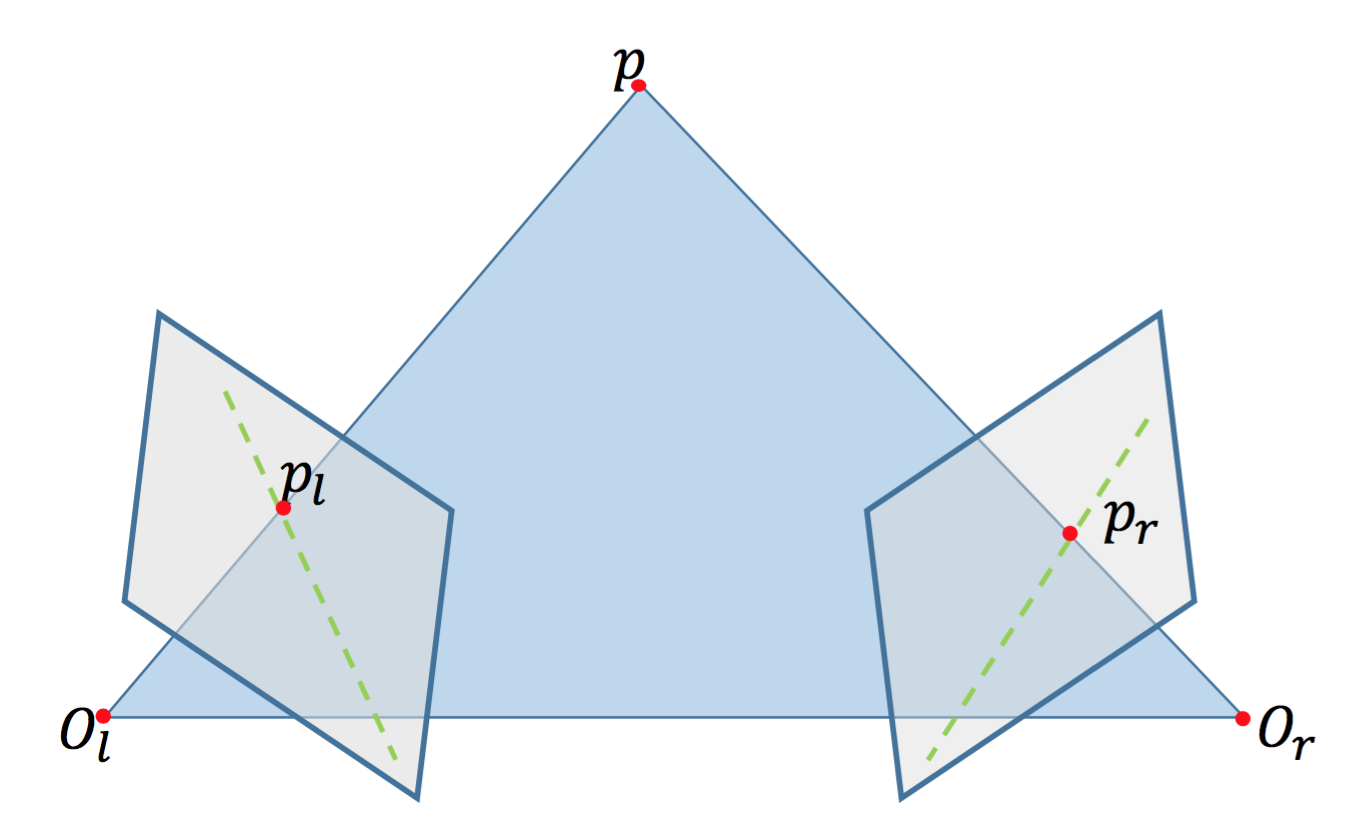
在图中，每台相机都有对应的投影中心$O_l$和$O_r$，对应相机的投影平面$\pi_r$和$\pi_l$，而点$p$、$O_r$和$O_l$所在的平面为极平面。
我们选择左相机$O_r$为中心坐标，另一个相机的原点坐标为$T$，则点$P$在左右相机观测到的坐标$P_r$和$P_l$之间满足：
$$P_r = R(P_l-T)$$
极平面可以表示为：
$$(P_l-T)^T(T\times P_l) = 0$$
由于叉积可以表示为反对称矩阵的点积，设向量$a = [a_1, a_2, a_3]$和$b = [b_1, b_2, b_3]$则两向量的叉积：
$$\begin{array}{cc} a\times b= \begin{bmatrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{bmatrix}\\
=(a_2b_3-a_3b_2)i + (a_3b_1-a_1b_3)j + (a_1b_2-a_2b_1)k=\left[\begin{array}{ccc}0&-a_3&a_2 \\ a_3&0&-a_1 \\ -a_2&a_1&0\end{array} \right]b\end{array}$$
所以有：
$$T\times P_l =SP_l= \left[\begin{array}{ccc}0&-T_z&T_y \\ T_z&0&-T_x \\ -T_y&T_x&0\end{array} \right]P_l$$
带入得到：
$$P_r^TRSP_l=0$$
其中本征矩阵$E=RS$而基础矩阵$F=(M_r^{-1})EM_l^{-1}$期中$M$为相机内参。

基础矩阵求解——八点法

由于极线约束，$q_r^TFq_l=0$转换有：

$$\begin{bmatrix}x_0 & y_0 & 1\end{bmatrix} \begin{bmatrix} F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33} \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ 1\end{bmatrix}$$
将其拆开得到：
$$\begin{bmatrix} x_0x_1 & x_0y_1 & x_0 & y_0x_1 & y_0y_1 & y_0 & x_1 & y_1 & 1\end{bmatrix} \begin{bmatrix} F_{11} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33} \end{bmatrix} = 0$$

这就类似于最小二乘方程$Ax = 0$
目标函数可以转换为：
$$ ||Ax|| = x^T(A^TA)x=\lambda^2||x||$$

所以对八点构成的$8 \times 9$矩阵进行SVD分解，$SVD(A)=[U,S,V]$取矩阵$V$最右奇异值向量为所求。
但是在实际计算过程中，匹配点坐标存在误差，我们需要将基础矩阵投影到真正的本征矩阵空间，可以另奇异值最后一个为0。